Math Talk (Lattice Multiplication)

You might be surprised why a Math hater like me would post something about the discipline. Well, this one is easy. I had a mix up of emotions -- happy yet embarrassed -- for discovering a new way of multiplying large numbers, but at least, it was never too late to have a knowledge of it. 

Let's talk about Lattice Multiplication. Lattice multiplication is a method of multiplying large numbers using a grid. This method breaks the multiplication process into smaller steps, which some students find easier. Digits to be carried are written within the grid, making them harder to miss. 

Had I not listened to that teacher in grade four discuss it, I might be, until now, an ignorant of Lattice Multiplication. That moment, I felt like fourth graders are smarter than me in Math. I tried to analyze the rulings and when I found out it was easy, I answered with the class. It was fun. Just follow these steps and you will know Lattice Multiplication in no time. (Well, of course except for those who already know how LM is done. *smile)

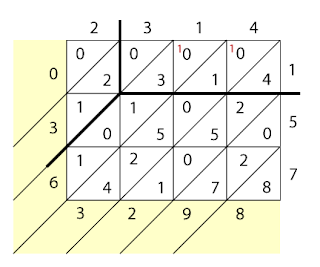
1. First, draw a grid that has as many rows and columns as the multiplicand and the multiplier. The grid shown here is for multiplying a 4-digit number by a 3-digit number.

 

2.  Draw a diagonal through each box from upper right corner to lower left corner. Continue the line a short way past the grid. 

 

3.  Write one factor across the top and the other down the right side, lining up the digits with the boxes. 

4. The multiplication is performed by multiplying the digits at the head of each row and column. Fill in each square of the grid with the product of the digits above and to its right, recording the products so that the tens are in the upper (diagonal) half of the square and the ones are in the lower half. If the product does not have a tens digit, record a zero in that triangle. 

In the example shown here, the highlighted row and column give us 1×5=5, so we write 0 in the upper half of the square and 5 in the lower half.

5. Now add the numbers in the grid along the diagonals, starting from the lower right corner. Carry any tens into the top of the next diagonal. 

In this example, the highlighted diagonal gives us 4+2+5+1=12, so we write 2 at the bottom of the diagonal and carry the 1 to the top of the next diagonal to the left.

6. To find the answer, read the digits starting down the left of the grid and continuing across the bottom. Here, the answer to 2314×157 is 363,298. 

 

7. Lattice multiplication can easily be extended to multiply decimal fractions. Suppose, instead of the above problem, we wanted to multiply 2.314 by 1.57. We would proceed as before, but draw lines from the decimal points down and to the left until they meet, then follow the diagonal to the left or bottom of the grid. The point where this diagonal emerges from the grid is the position of the decimal point in the answer.

I know you will not read 'til the end part of this post because for you, long posts are boring. hahaha. I understand. I also understand if you will not drop a comment. Anyway, have a good day, Lattices :)